Прогнозирование временных рядов методом муравьиных колоний
Привет.
Я хочу рассказать об одной задаче, которая очень заинтересовала меня в свое время, а именно, о задаче прогнозирования временных рядов и решении этой задачи методом муравьиного алгоритма.
Для начала вкратце о задаче и о самом алгоритме:
Прогнозирование временных рядов подразумевает, что известно значение некой функции в первых n точках временного ряда. Используя эту информацию необходимо спрогнозировать значение в n+1 точке временного ряда. Существует множество различных методов прогнозирования, но на сегодняшний день одними из самых распространенных являются метод Винтерса и ARIMA модель. Подробнее о них можно почитать тут.
О том что такое муравьиный алгоритм говорилось уже довольно много. Для тех кому лень лезть, например, сюда, перескажу. Вкратце, муравьиный алгоритм это моделирование поведения муравьиной колонии в их стремлении найти кратчайший путь к источнику еды. Муравьи, при движении оставляют за собой след феромона, который влияет на вероятность выбора муравьем данного пути. Учитывая то, что муравьи будут за один и тот же промежуток времени пройти короткий путь бОльшее количество раз, на нем будет оставаться больше феромона. Таким образом, с течением времени, все больше муравьев будут выбирать кратчайший путь к источнику пищи.
Для наглядности, вставлю картинку:
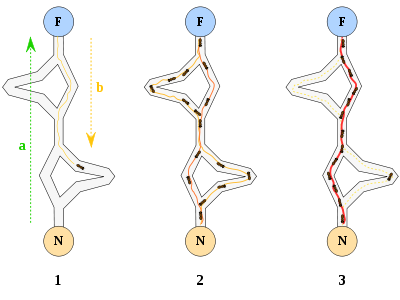
Теперь, перейдем непосредственно к решению задачи прогнозирования методом муравьиных колоний.
Первая проблема с которой мы сталкиваемся — необходимо представить временной ряд в виде графа, на котором будем запускать муравьиный алгоритм.
Было найдено два возможных решения:
1. Представить временной ряд в виде мультиграфа где из каждой точки временного ряда можно перейти в каждую набором определенных приростов. (Для облегчения задачи будем брать нормализованные значения на промежутке от -1 до 1). Это был первый подход, который мы попробовали. Он показал неплохой результат на временных рядах малой размерности, но с увеличением размерности стала резко падать как точность прогноза, так и производительность, поэтому от этого варианта отказались.
2. Представить временной ряд в виде набора сцепленых графов, где каждый граф отвечает за свою величину прироста значения временного ряда. иначе говоря, имеем граф который отвечает за прирост -1, -0,9… и так до 1. Шаг, естественно, можно уменьшить, или увеличить, что скажется на точности прогноза и ресурсоемкости задачи.(в конечном итоге этот вариант оказался наиболее удачным.)
На этом наборе сцепленных графов, запускался муравьиный алгоритм(на каждом графе свой), который откладывал феромон на ребрах, соответствующих известным значениям временного ряда. Причем, при откладывании феромона на графе i, феромон также откладывался на графах i-1и i+1, но в гораздо меньшем количестве(в нашем случае 1/10 от базового количества феромона) таким образом, муравьи выделяли наиболее часто встречающиеся последовательности прироста значения временного ряда, а за счет откладывания феромона на смежные графы, нивелировалась возможная погрешность и изначальная зашумленность временного ряда.
Данный алгоритм мы тестировали на искусственно подготовленных временных рядах с разным уровнем периодичности и шума. Результат получился двояким. С одной стороны, при уровнях шума до 0,3 алгоритм показывает высокие результаты прогноза, сравнимые с результатами ARIMA модели. На более высоких уровнях шума возникает большой разброс результатов: прогноз то очень точный, то совершенно неправильный.
В настоящий момент мы работаем над подбором оптимального значения параметров алгоритма и некоторыми методами его улучшения, о которых я напишу как только они будут в достаточной степени проверены.
Спасибо всем за внимание.
Я хочу рассказать об одной задаче, которая очень заинтересовала меня в свое время, а именно, о задаче прогнозирования временных рядов и решении этой задачи методом муравьиного алгоритма.
Для начала вкратце о задаче и о самом алгоритме:
Прогнозирование временных рядов подразумевает, что известно значение некой функции в первых n точках временного ряда. Используя эту информацию необходимо спрогнозировать значение в n+1 точке временного ряда. Существует множество различных методов прогнозирования, но на сегодняшний день одними из самых распространенных являются метод Винтерса и ARIMA модель. Подробнее о них можно почитать тут.
О том что такое муравьиный алгоритм говорилось уже довольно много. Для тех кому лень лезть, например, сюда, перескажу. Вкратце, муравьиный алгоритм это моделирование поведения муравьиной колонии в их стремлении найти кратчайший путь к источнику еды. Муравьи, при движении оставляют за собой след феромона, который влияет на вероятность выбора муравьем данного пути. Учитывая то, что муравьи будут за один и тот же промежуток времени пройти короткий путь бОльшее количество раз, на нем будет оставаться больше феромона. Таким образом, с течением времени, все больше муравьев будут выбирать кратчайший путь к источнику пищи.
Для наглядности, вставлю картинку:

Теперь, перейдем непосредственно к решению задачи прогнозирования методом муравьиных колоний.
Первая проблема с которой мы сталкиваемся — необходимо представить временной ряд в виде графа, на котором будем запускать муравьиный алгоритм.
Было найдено два возможных решения:
1. Представить временной ряд в виде мультиграфа где из каждой точки временного ряда можно перейти в каждую набором определенных приростов. (Для облегчения задачи будем брать нормализованные значения на промежутке от -1 до 1). Это был первый подход, который мы попробовали. Он показал неплохой результат на временных рядах малой размерности, но с увеличением размерности стала резко падать как точность прогноза, так и производительность, поэтому от этого варианта отказались.
2. Представить временной ряд в виде набора сцепленых графов, где каждый граф отвечает за свою величину прироста значения временного ряда. иначе говоря, имеем граф который отвечает за прирост -1, -0,9… и так до 1. Шаг, естественно, можно уменьшить, или увеличить, что скажется на точности прогноза и ресурсоемкости задачи.(в конечном итоге этот вариант оказался наиболее удачным.)
На этом наборе сцепленных графов, запускался муравьиный алгоритм(на каждом графе свой), который откладывал феромон на ребрах, соответствующих известным значениям временного ряда. Причем, при откладывании феромона на графе i, феромон также откладывался на графах i-1и i+1, но в гораздо меньшем количестве(в нашем случае 1/10 от базового количества феромона) таким образом, муравьи выделяли наиболее часто встречающиеся последовательности прироста значения временного ряда, а за счет откладывания феромона на смежные графы, нивелировалась возможная погрешность и изначальная зашумленность временного ряда.
Данный алгоритм мы тестировали на искусственно подготовленных временных рядах с разным уровнем периодичности и шума. Результат получился двояким. С одной стороны, при уровнях шума до 0,3 алгоритм показывает высокие результаты прогноза, сравнимые с результатами ARIMA модели. На более высоких уровнях шума возникает большой разброс результатов: прогноз то очень точный, то совершенно неправильный.
В настоящий момент мы работаем над подбором оптимального значения параметров алгоритма и некоторыми методами его улучшения, о которых я напишу как только они будут в достаточной степени проверены.
Спасибо всем за внимание.